In a previous post, we looked at a model as a (imperfect) representation of a physical phenomenon, the behavior of a collection of gas molecules. In this post, we are going to explore what a model is in the context of machine learning.

The goal of devloping a machine learning model is to be able to make predictions. In other words, if we have a set of observations (i.e. our data), what would we predict for a new observation? The model is the function, algorithm or process by which we make predictions based on previous observations (i.e. training data).

A simple example

As a simple illustration of what a model is, let’s consider a very famous dataset called the Fisher Iris Dataset - it’s used extensively throughout statistics and machine learning as a kind of “hello, world” of datasets! In fact, it’s so famous that it is included with each MATLAB installation:

load fisheriris

Image from Galaxy 101 for Everyone

It consists of measurements of 150 samples of three different iris flower species. Each observation contains measurements of petal length and width and sepal length and width. Here, we are going to explore the relationship between petal length and petal width.

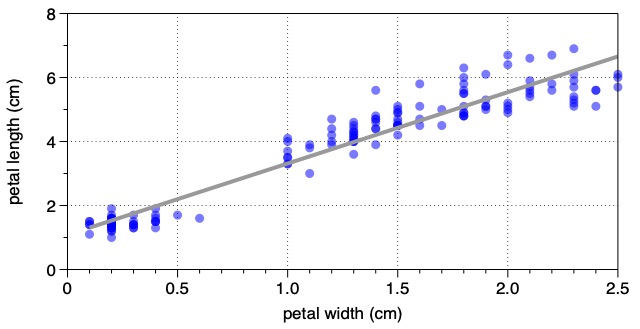
As you can see, there is a correlation visible: larger petal lengths tend to be associated with larger petal widths. The relationship is not perfect, there is scatter amongst the data. Nonetheless, you can see an upward trend in the data points.

And that’s a model! Yes, that simple line represents a model that generalizes a relationship between the two measurements. We can use that line (ahem … model) to predict the length of any new petal for which we have measured the width.

Now, we know that the model is a line (technically, a linear regression) with the functional form:

where $m$ is the slope and $b$ is the intercept.

But, could we specify more about this model? For example, how many inputs and outputs are there? Not only is it a linear regression, but it has one input ($x$=petal width) and one output ($y$=petal length). Thus, the term “model” might be used to include that information, as well.

Furthermore, “model” might include the specific values of the model parameters describing the best-fit line: the slope and the intercept. In other words, the model might be: a linear regression with one input and one output and values of $m = 2.23$ and $b = 1.08$ cm.

The model in this example is a type of regression model. That is, it makes a numerical prediction about the value of a specific quantity based on the input data. A different type of model, a classification model, is used not to predict a value of something but to predict to which group, or class, a sample belongs.

We’ll explore the differences between these two types of models in an upcoming post …